1.　DRYの接触セッショク圧力アツリョク分布ブンプの計算

弾塑性有限要素(FEM)による球面軸受の計算例を示します。

更に、次の計算結果を比較します。

(1) 球面相互の隙間を2次式で近似したヘルツ面圧の計算 (BEM1)

隙間 g は次式で与えられます。r は原点からの距離です。また Ru=10, Rd=10.05 です。

g(r) = r^2/(2・Ru) - r^2/(2・Rd)

(2) 球面相互の隙間を正確に計算した半無限体近似による面圧の計算 (BEM2)

隙間 g は次式で与えられます。r は原点からの距離です。また Ru=10, Rd=10.05 です。

g(r) = Ru - (Ru^2 - r^2)^0.5 - [ Rd - (Rd^2 - r^2)^0.5 ]

(3) 塑性変形を無視した弾塑性有限要素法による計算 (FEM-LINEAR)

(4) 塑性変形を考慮した弾塑性有限要素法による計算 (FEM-NON.LINEAR)

計算条件は次の通りです。

ヤング率　　E = 206     GPa

ポアソン比　ν=0.3

降伏点　　　σy = 300　MPa

K 値　　　　 K =100    MPa

m 値　　　　 m = 1

垂直荷重   Fz = 30    KN

σy, K, m の値は塑性変形を考慮した弾塑性有限要素法による計算でだけ有効です。

この時、変形抵抗 H は相当塑性歪εp の関数として次のように表されると仮定しました。

H(εp) = σy + K・(εp)^m

FEMの計算では下部球殻の下面（青色部）のXYZ座標を拘束しました。

FEMの計算では上部球殻の上面（赤色部）のXYZ座標を拘束して姿勢を保ったまま荷重が釣合うまで

下方に押しました。

下部球殻の上面と上部球殻の下面（緑色部）が接触面です。

半無限体近似(BEM)の計算では下部の無限遠下方が支持されています。

最大面圧 Pmax と接近量δは次のようになりました。

最大面圧 Pmax(MPa)

接近量δ(mm)

BEM1

264.417

0.0269623

BEM2

302.825

0.0297371

FEM-LINEAR

437.291

0.0155244

FEM-NON.LINEAR

416.554

0.0157115

BEMの結果とFEMの結果はかなり異なります。FEMの方が正確です。

このような計算では半無限体近似の誤差が大きいことが分かります。

BEMでは無限遠を支えているためにFEMよりも接近量が大きく面圧が低いです。

BEM2では接触面積が狭くなるためにBEM1よりも面圧が高いです。

FEM-NON.LINEARでは塑性変形によって応力緩和するためにFEM-LINEARよりも面圧が低いです。

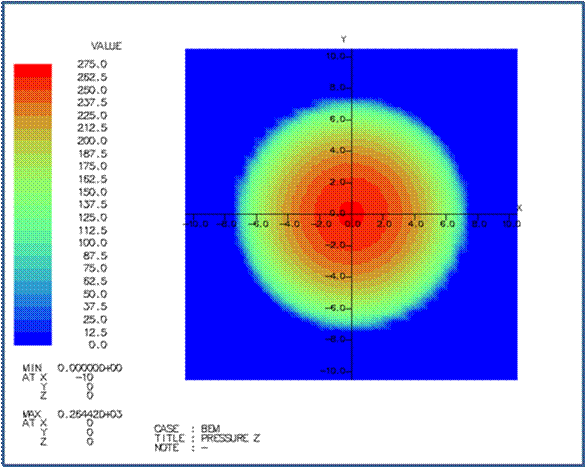
(1) 球面相互の隙間を2次式で近似したヘルツ面圧の計算の結果は次の通りです。

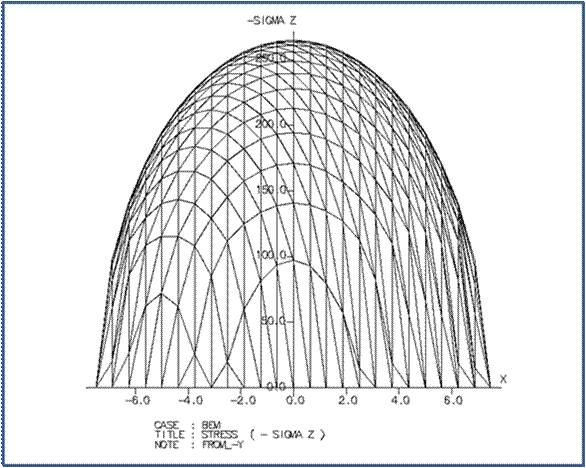
(2) 球面相互の隙間を正確に計算した半無限体近似による面圧の計算の結果は次の通りです。

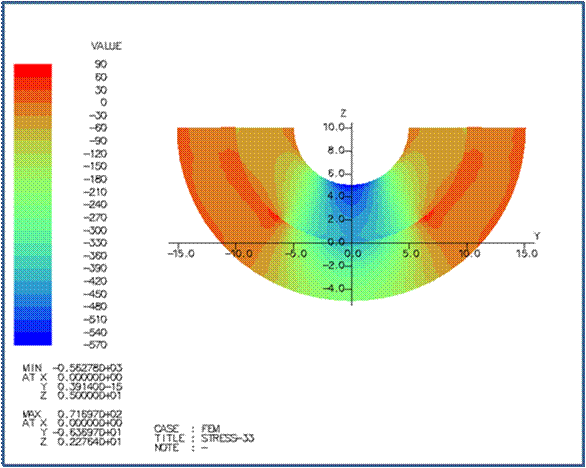
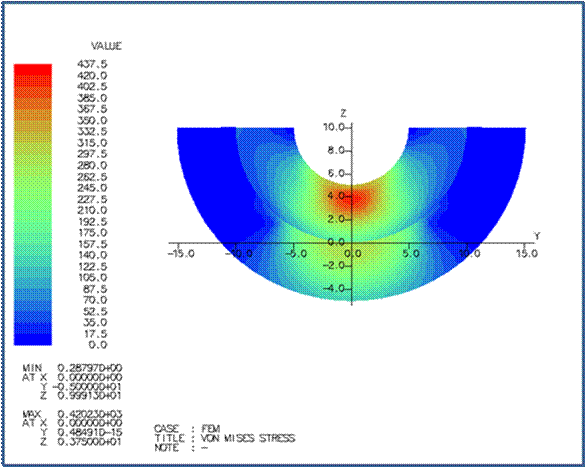
(3) 塑性変形を無視した弾塑性有限要素法による計算の結果は次の通りです。

X=0 断面のσ33 とミゼスの応力の分布は次の通りです。

(4) 塑性変形を考慮した弾塑性有限要素法による計算の結果は次の通りです。

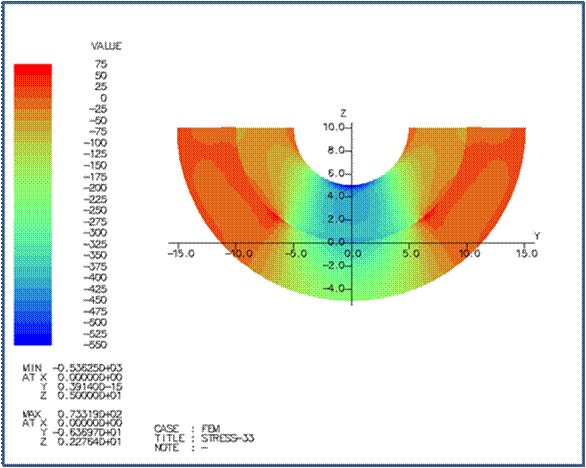
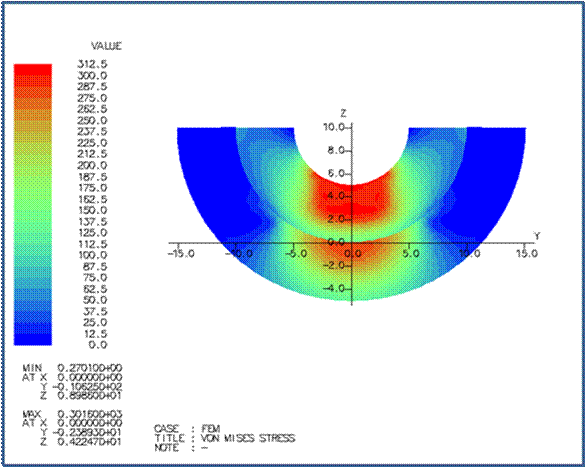
X=0 断面のσ33 とミゼスの応力の分布は次の通りです。

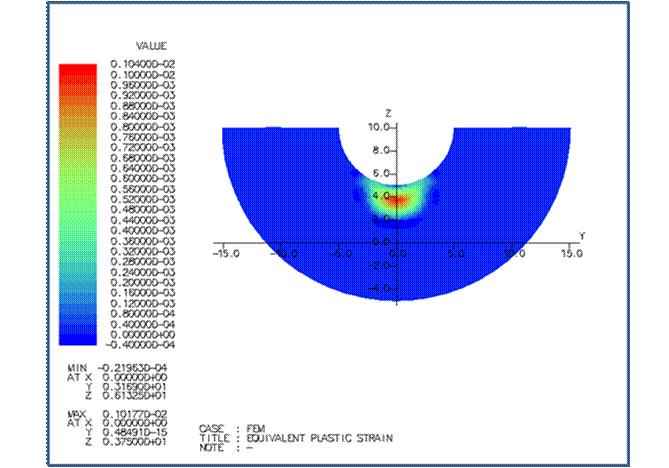
X=0 断面の相当塑性ひずみの分布は次の通りです。