|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![78. ��������ɂ��]�����R�̌v�Z](tedcpa_example78.files/image036.gif)
|
|
|
| �@1.�@DRY���ڐG�������z�̌v�Z |
|
|
|
��������ɂ��]�����R�̌v�Z��������܂��B |
|
|
|
�v�Z�����͎��̂Ƃ���ł��B |
|
|
|
�{�[�����a �F10 mm |
|
�����d Fz = 5000 N |
|
|
���O�����a �F20 mm |
|
�����O�� E = 206 Gpa |
|
|
�O�O�����a �F30 mm |
|
�|�A�\���� ��= 0.3 |
|
|
���֍a���a �F5.2
mm |
|
���薀�C�W�� ��= 0.2 |
|
|
�O�֍a���a �F5.2
mm |
|
���֑��x Vxi = 1000 mm/sec |
|
|
|
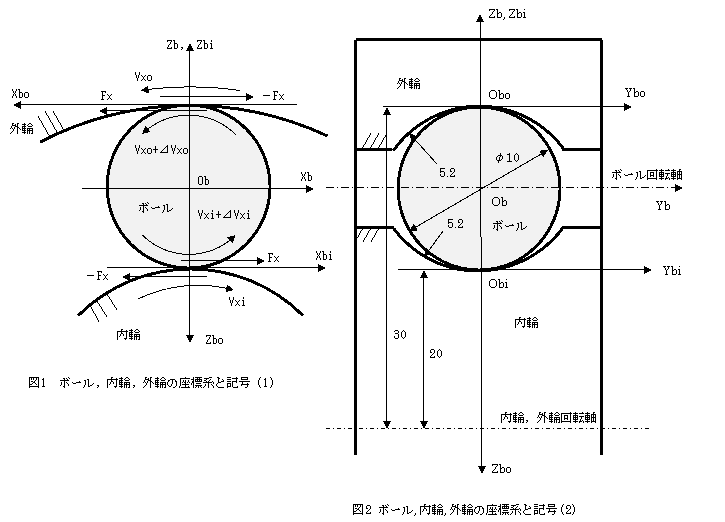
�`��ƍ��W�n�͉��}�̂Ƃ���ł��B�{�[���̒��S�͐Î~���Ă��܂��B |
|
|
�O�ւ͂����ނ˓��ւ̋t�����ɉ�]���Ă��܂��B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�n�߂ɓ]�����R�̖͎��I�Ȑ����������B�}�R�C�}�S�C�}�T�̓{�[���Ɠ��ւ̐ڐG�̗l�q������������ |
|
|
�ł���B�{�[���̉�]�p���x��b�Ɠ��ւ̉�]�p���x��r�͈��ł���Ƃ���B�}�R�Ɏ����悤�ɐڐG |
|
|
�ʂ��p�Ȃ��Ă��邽�߂ɏ��]����̐������Ƃ��ē����ł̓{�[���̑��x
ri�E��b�������A�O���ł͓��� |
|
|
�̑��x
Ro�E��r�������B���]����̐���ł̓{�[���̑��xr�E��b�Ɠ��ւ̑��xR�E��r �͓������B�{�[�� |
|
|
�ɓ������C��Px�͎��̂悤�ɗ^������B |
|
|
|
���]����̐��̓����ł� Px = �|�ʁEPz �@ |
|
|
���]����̐��̊O���ł� Px = �{�ʁEPz �A |
|
|
|
�����Ńʂ͊��薀�C�W���APz�͐����ڐG���͂ł���B�}�T�Ɏ����悤�ɏ��]����̐��̓����̗̈�� |
|
|
Si�C�O���̗̈��So�Ƃ��A���ꂼ��̗̈�ɓ������C�͂�Fxi�CFxo�Ƃ���BFxi�CFxo�͎��̂悤�ɗ^���� |
|
|
���B |
|
|
|
Fxi = ��si Px ds �B |
|
|
Fxo = ��so Px ds �C |
|
|
|
���̂Q�̖��C�͂��ލ����Ă���Ɖ��肷��Ύ�������������B |
|
|
|
Fxi = �|Fxo �D |
|
|
|
���C��Fxi��Fxo���{�[���ɋy�ڂ����[�����g���l����B�}�R�Ɏ����悤�Ƀ{�[����]������Fxi�̉d�d |
|
|
�S�܂ł̋�����ri�Ƃ��A�{�[����]������Fxo�̉d�d�S�܂ł̋�����ro�Ƃ���B���炩�� |
|
|
|
ri > ro �E |
|
|
|
�ł���B�{�[���Ɋ|����{�[����]���iYb���j���̃��[�����gMi�͎����ŗ^������B |
|
|
|
Mi = Fxo�Ero �{ Fxi�Eri = Fxo�E( ro �| ri
) < 0�@ �F |
|
|
|
�{�[���Ɋ|���郂�[�����gMi�͂O�łȂ���Ȃ�Ȃ�����A�D�����������Ȃ����ƂɂȂ�B���Ȃ킿���� |
|
|
�C��Fx�� |
|
|
|
Fx = Fxi �{ Fxo�@�� 0�@�@ �G |
|
|
|
����Fx���]�����R�ł���B�ڐG�ʂ��p�Ȃ��Ă���ꍇ�ɂ͖��C�͂̒ލ������ƃ��[�����g�̒ލ��� |
|
|
������v���Ȃ����Ƃ��킩��B |
|
|

|
|
|
|
�]�����R�̌v�Z�菇�������B |
|
|
|
�}�P�Ɛ}�Q�̓{�[���Ɠ��O�ւ̐ڐG�̍��W�n�ƋL���������Ă���BObi,
Xbi, Ybi, Zbi �̓{�[���Ɠ��ւ� |
|
|
�ڐG�v�Z���W�n�ł���BObo, Xbo, Ybo, Zbo
�̓{�[���ƊO�ւ̐ڐG�v�Z���W�n�ł���B�{�[���̒��S |
|
|
Ob���Î~���Ă�����W�n�ōl����B���Ȃ킿�A�O�ւ̑��xVxo�͂����ނ˓��ւ̑��xVxi�̋t������ |
|
|
����B�ڐG�ʂ��p�Ȃ��Ă��邽�߂ɐڐG�_Obi�ł̓{�[���̕������ւ����������x�������B���̊��� |
|
|
���x����Vxi�Ƃ���B���l�ɐڐG�_Obo�ł̓{�[���̕����O�ւ����������x�������B���̊��葬�x�� |
|
|
��Vxo�Ƃ���B�v�Z�菇�͎��̒ʂ�ł���B |
|
|
|
(A) �{�[���̊��葬�x��Vxi�����肷��B |
|
|
�����ł͇�Vxi = 17, 17.5, 18 mm/sec �Ƃ����B |
|
|
|
(B)
�����dFz���|���āA�{�[���Ɠ��ւ̓]����ڐG�̌v�Z�����s����B���̌v�Z�ɂ���ē]�����R |
|
|
Fx��Ball��Yb�����Ɋ|���郂�[�����gMi�����߂邱�Ƃ��ł���BFx��Mi�͇�Vxi�̊��ł���B |
|
|
|
(C)
�����dFz��(B)�ŋ��߂��]�����RFx���|���ă{�[���ƊO�ւ̓]����ڐG�̌v�Z�����s����B�{ |
|
|
�[���ƊO�ւ̊��葬�x��Vxo��Ball��Yb�����Ɋ|���郂�[�����gMo�����߂邱�Ƃ��ł���B |
|
|
��Vxo��Mo�͇�Vxi�̊��ł���BFz��Fx��(B)�̏ꍇ�Ƌt�����ł��邩��Z������X�����̗͂� |
|
|
�ލ������ƂɂȂ�B |
|
|
|
(D)
�{�[����Yb�����Ɋ|����S���[�����gM���v�Z����BM�͎����ŗ^������B |
|
|
|
M = Mi �{ Mo �H |
|
|
|
M�͇�Vxi�̊��ł���BM(17), M(17.5), M(18)
�����߂�B |
|
|
|
(E)
�{�[���Ɋ|����S���[�����g�͂O�łȂ���Ȃ�Ȃ����玟������������B |
|
|
|
M(��Vxi) = 0 �I |
|
|
|
�I������������悤�ɇ�Vxi�߂���B |
|
|
3�_ ( 17, M(17) ) , ( 17.5, M(17.5)
) , ( 18, M(18) ) ��ʂ�Q���Ȑ�����M(��Vxi) = 0 �ƂȂ釙Vxi |
|
|
�����߂�B�����ł͇�Vxi = 17.41604 mm/sec
�ł��邱�Ƃ��킩�����B |
|
|
|
(F) ��Vxi = 17.41604 mm/sec �Ƃ���(B),
(C) �̌v�Z�����s����B |
|
|
|
����Ń{�[���Ɋ|����XZ�����̉dFx,
Fz��Yb���܂��̃��[�����gM�͂��ׂĒލ������ƂɂȂ�B���� |
|
|
�ȊO�̉d�A���[�����g�͌��X�O�ł���B(F)�ŋ��߂�ꂽFx���]�����R�ł���B�]���薀�C�W����R�� |
|
|
�����ŗ^������B |
|
|
|
��R = Fx / Fz �J |
|
|
|
�v�Z���ʂ͎��̒ʂ�ł���B |
|
|
|
�]�����R Fx =�@ 17.70560509 N |
|
|
�]���薀�C�W�� ��R = �@0.0035411 |
|
|
���葬�x ��Vxi = �@17.41604 mm/sec |
|
|
���葬�x ��Vxo = �@12.02412 mm/sec |
|
|
�O�ւ̑��x Vxo = �@1005.39192 mm/sec |
|
|
�i�{�[�����S���Î~���Ă��鎞�A���ւ��O�ւ��������x���j |
|
|
|
�]���薀�C�W���͊��薀�C�W�������Q���������B |
|
|
|
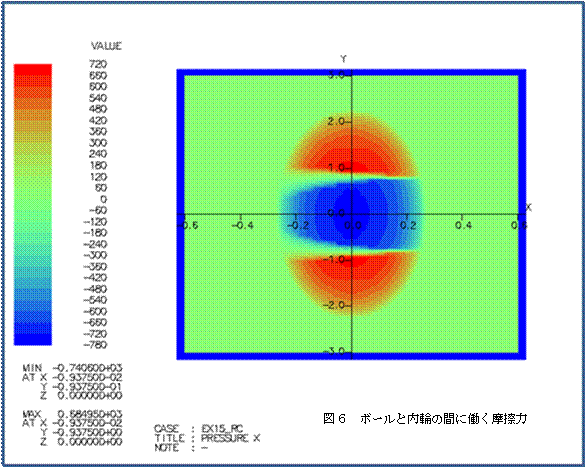
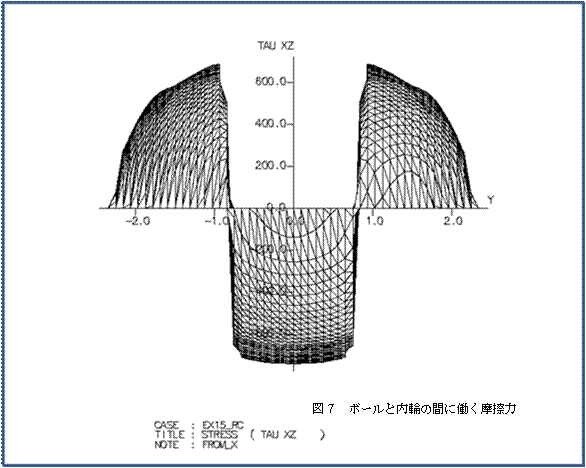
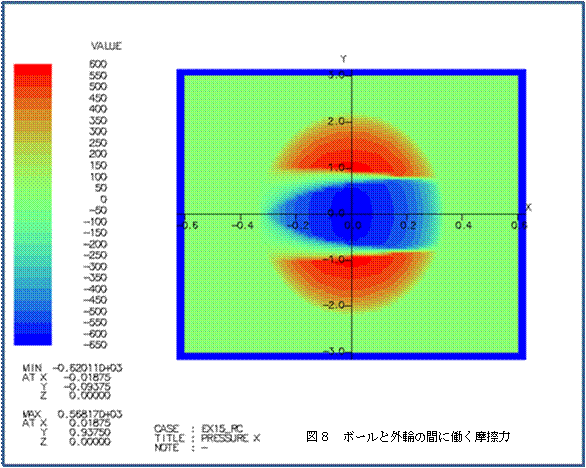
�}�U�Ƀ{�[���Ɠ��ւ̊Ԃɓ������C�͂̓������}�A�}�V�ɓ����f�[�^��X���������猩�����b�V���}�A |
|
|
�}�W�Ƀ{�[���ƊO�ւ̊Ԃɓ������C�͂̓������}�������B |
|
|
���]����̐��͂��ݍ����n�ߑ��ōL���ڂ₯�Ă���B���ݍ����I�葤�ŋ����V���[�v�ł���B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Page
Top�� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|