|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
| 1. DRYの接触圧力分布の計算 |
|
|
|
ジャーナル軸受のスクイーズの計算例と非定常理論解との比較を示します。 |
|
|
|
静止したジャーナル軸受の軸を軸受と同心位置に置き、荷重を掛けない状態で流体を充満させます。 |
|
|
その後、急激に大きな荷重を掛けます。軸は時刻と共に少しづつ沈みます。 |
|
|
|
理論解と比較し、非常に良く一致することを確認しました。 |
|
|
|
計算条件は次のとおりです。 |
|
|
|
軸受長さ |
|
L |
|
50, ∞ |
|
mm |
|
|
軸受半径 |
|
R |
|
25 |
|
mm |
|
|
半径クリアランス |
C |
|
0.1 |
|
mm |
|
|
荷重 |
|
W |
|
0 → 1000 |
|
N |
|
(下図を参照ください) |
|
|
粘性係数 |
|
μ |
|
500・10-9 |
|
MPa・sec |
(圧力に依存しない) |
|
|
|
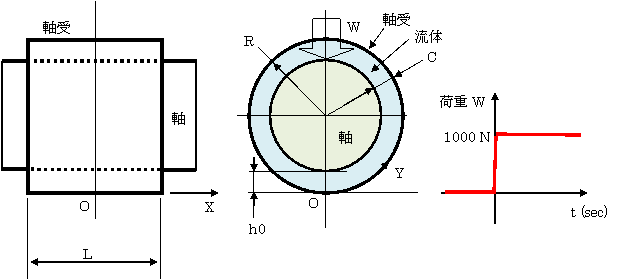
形状と座標系は下図のとおりです。Y座標は軸受の周に沿って測った長さです。 |
|
|
|
|
|
|
最小油膜厚さ h0 と偏芯率εの関係は次の通りです。 |
|
|
|
h0 = C - C・ε |
|
|
|
L = ∞ の場合のこの問題には理論解があります。 |
|
|
Theory of hydrodynamic lubrication,
Oscar Pinkus, University Microfilms, P221 |
|
|
偏芯率εは時刻 t
の関数であり、その関係は次式で与えられます。(上記図書の(7-21)式を積分します。) |
|
|
t = 12・πμLC / [ W・(C/R)^3
]・tan(asin(ε)) |
|
|
|
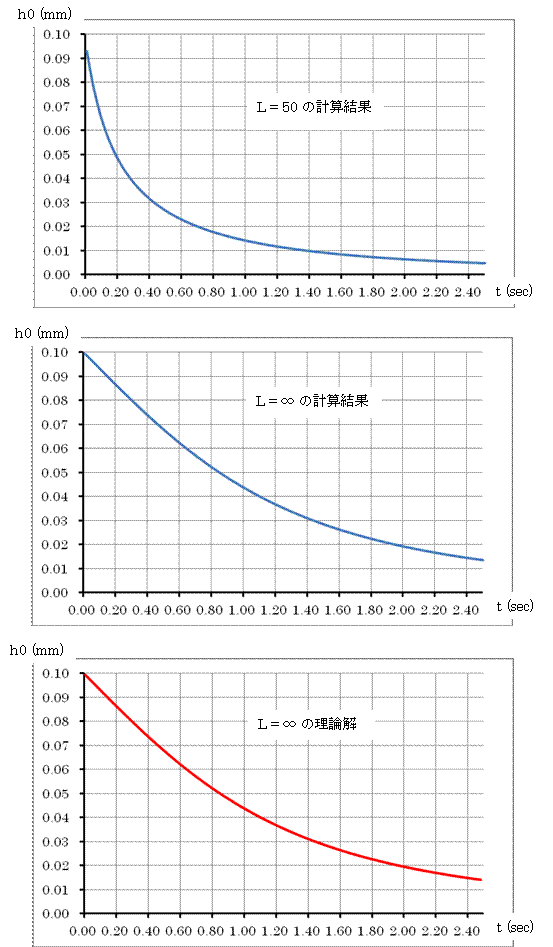
0 < t ≦ 2.5 sec を200等分して計算しました。 |
|
|
|
計算結果を示します。L=∞
の計算結果と理論解は非常に良く一致していることが分かります。 |
|
|
全く異なる計算方法であるにもかかわらずこれだけ良く一致するのは奇跡的にも思えます。 |
|
|
TED/CPAの計算の確かさを示しています。 |
|
|
|
L=50
の計算結果をみると、流体が軸受端部から漏れるために無限幅軸受と比較して早く油膜が薄くなる |
|
ことがわかります。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
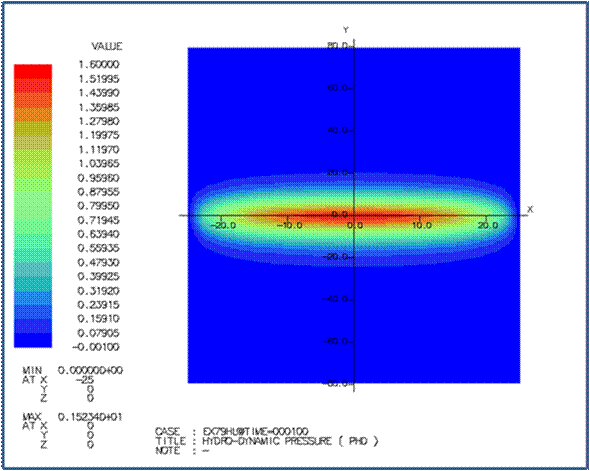
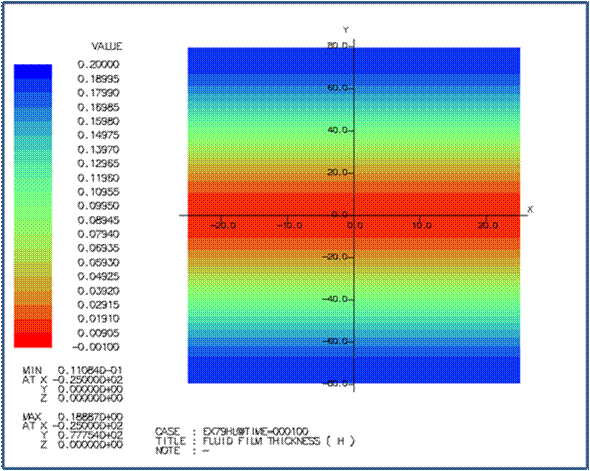
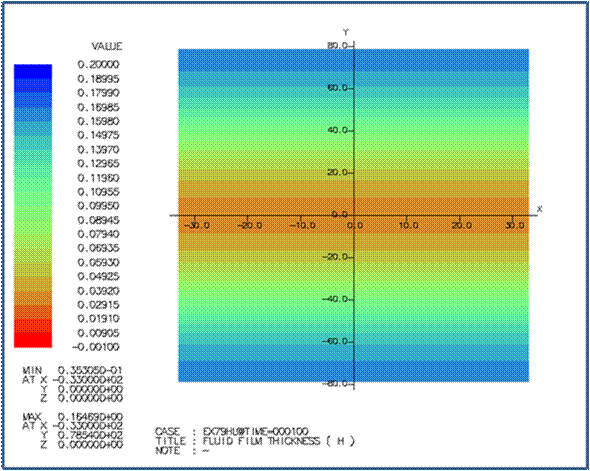
L=50 の場合の時刻カウント 100
での流体潤滑圧力と油膜厚さは次の通りです。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
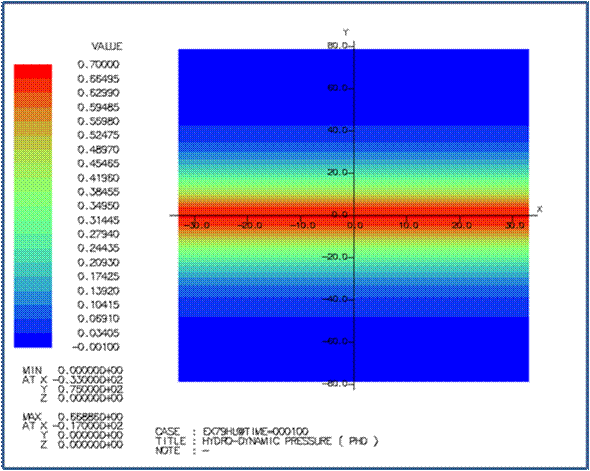
L=∞ の場合の時刻カウント 100
での流体潤滑圧力と油膜厚さは次の通りです。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Page
Topへ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|